导读：在《揭示宇称变换的真面目》一文中，我们明确指出：现有理论中的宇称变换，并不是空间反演下的波函数变换，它其实只是检测波函数“奇偶性”的简单操作而已。我们在文中坦陈，我们面临一个不容回避的挑战性课题：空间反演下，波函数究竟该如何变换？正确的波函数变换公式又到底是什么？并且承诺“将撰另文加以讨论”。
如今面世的本文，就是我们言而有信交出的原创性答卷。我们先是亮出自己找到的波函数变换公式；再是提出一个检验上述公式是否成立的试金石，并给出我们的检验结果：我们的波函数变换公式，能够成立。而宇称变换公式，则被再一次证伪。
文中不得不援用的13个公式，相信高中的理科学生应该能看懂。
我们曾经提到过，空间反演的同义词，叫做左右变换。对一般读者来说，“空间反演”显得专业、抽象，而“左右变换”则比较接地气。事实上，一个人只要去照镜子，就会对左右变换产生形象化的亲身体悟：明明自己是用右手在刷牙，而镜子里的“自己”却共时地用其左手在刷牙。在本文的论述中，我们用左右变换来替代空间反演，祈望能有助于读者对文本的阅读和理解。
我们知道，在高中数学教科书中，有关于空间坐标平移变换和旋转变换的内容。而左右变换，则是空间坐标的另一种变换——反射变换，它与镜像反映实质上是一回事[1]。反射变换的一般形式，可用矢径r的变换表示如下：
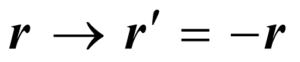(1)
人们进行坐标变换，自然不是在玩数学游戏，而是为了探究物理规律的各种对称性。式(1)所示的左右变换，就是奔研讨左右对称性而去的。如同空间坐标的平移和旋转变换那样，左右变换也会导致各种物理量的相应变换，其中包括量子世界中的重要物理量——波函数的变换。现有理论中的“宇称变换”公式，就被称为“左右变换下物理量变换”的通用公式；其中的重头戏，则是微观粒子或粒子体系波函数之变换。
不过，在《揭示宇称变换的真面目》[2]一文中，我们明确指出：现有理论中的宇称变换，其实并不是左右变换下的波函数变换，它只是检测波函数“奇偶性”的简单操作而已。我们并且坦陈，我们面临一个不容回避的挑战性课题：左右变换下，波函数究竟该如何变换？正确的波函数变换公式又到底是什么？
在《空间反演下的物理量变换与左右对称性》[3]这篇论文中，我们已经给出了自己独立探索的结果。在我们的专著《物理学分立对称性新论》[4]中，我们又做了重申。我们在本文中要做的，是推介我们的上述原创性成果：我们将首先亮出自己找到的波函数变换公式，再是公示一个检验上述公式是否成立的试金石，并报告我们的检验结果。
在写作这篇推介文章的过程中，出乎我们意料的是，我们居然又有了喜人的新斩获。现在，本文中“我们找到的波函数变换公式”，已不是载于文献[3]和[4]中的公式，而是刚刚新鲜出炉的公式。
一、我们找到的波函数变换公式
我们独立探索的着眼点是：一般情况下，波函数乃是复数。那么，左右变换会对复数造成影响吗？如果有影响，又将体现在哪里？
为了写作此文，我们重温了一本大学教科书——《复变函数》[5]。我们在浏览复数的四种表示法时[6]，突然顿悟到：如果从复数的矢量表示法着手，就能简洁明快、单刀直入地找到波函数的变换公式。
常用的复数表示法，叫做点表示法：任一复数 
与一对有序实数x、y相对应，故对于平面上给定的直角坐标系，可用坐标为 (x , y) 的点来表示这一复数。x轴称为实轴，y轴称为虚轴，两轴所在的平面称为复平面或z平面。而复数的矢量表示法是：复数z还能用复平面上从原点指向点(x , y) 的矢量来表示（图1）。矢量的长度称为z的模或绝对值，记作
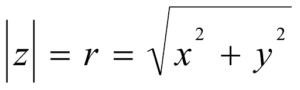(2)
图1 复数的矢量表示法
复数z既然是矢量，那么在左右变换下，它的变换关系就与式(1)所示的坐标变换关系相同，即有
. 
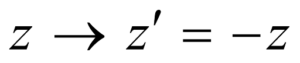(3)
这就是说，左右变换把任一复数z变换成其相反数-z。
由此立马可知，作为矢径r和时间t 的函数的任一波函数
，将在左右变换下作如下变换：
. 
(4)
这里，我们要破例提一下空间反演；空间反演的英文表达是：Space Inversion，我们取其首字母S作为算符标识，以算符
表示上述变换：
. 
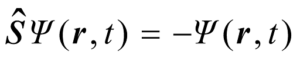(5)
我们把算符郑重地命名为波函数的左右变换算符，而式(5)就是我们找到的左右变换下的波函数变换公式。
现在，很有必要把宇称变换公式重述如下：
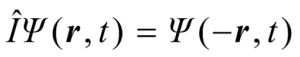(6)
式(6)为现有理论中的左右变换下的波函数变换公式。不过，式中的宇称算符
，不光仅对波函数适用，它更是左右变换下通用的物理量变换算符；其功能是：把物理量函数中的空间坐标改变符号，从而实现对该物理量的“变换”。
式(5)与式(6)看上去差别不大，但实质上截然不同。此刻，两个公式面临一场真假美猴王般的对决：左右变换下的波函数变换，究竟是由算符来表征，还是由算符来表征？式(5)与式(6)，到底哪个为真家伙？哪个又是冒牌货呢？
二、一块检验真假的试金石
所幸的是，我们很快就找到了一块试金石，那就是：微观粒子在空间各处的几率分布函数w(r,t)。w(r,t)可是一个响当当的标量，它在左右变换时保持不变：
. 
(7)
让我们先来看看，采用我们的式(5)作为波函数的变换公式时，w(r,t)是否果然为标量。
对于一个粒子而言，表征波之强度的波函数模的平方，与t时刻在空间r处单位体积内发现粒子的几率成正比[7]；而对于归一化的波函数，则比例系数为+1，即有
. 
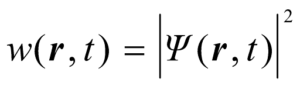(8)
由上式可知，在左右变换下，w(r,t)将作如下变换
. 
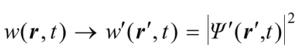(9)
对式(5)来说，式(9)中的
就是-。显然，我们总有
， 
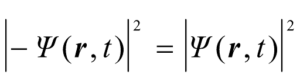(10)
即总有
. 
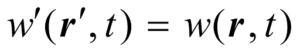(11)
式(11)雄辩地表明，从我们的式(5)出发，粒子的几率分布函数w(r,t)的确是标量，它在左右变换下持守金刚不败之身。
一句话，我们的波函数左右变换算符，经受住了试金石的检验。
接着让我们来看看，人们采用大名鼎鼎的式(6)时，w(r,t)是否为标量。
对式(6)来说，式(9)中的乃是
。我们要问：人们能总有
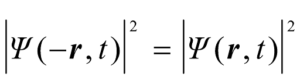(12)
吗？即人们总能得到式(11)吗？
显然，人们不是总能得到式(11)。对于具有“奇偶性”的波函数：
, (13)
人们的确能有式(12)，从而得到式(11)。而对于非“奇”非“偶”之波函数，人们就只能徒呼无奈，无从觅得式(12)、无法得到式(11)了。
这就是说，在宇称变换下，粒子在空间各处的几率分布函数w(r,t)一般地不能保持不变，w(r,t)也就随之失去了作为标量的资格。
一句话，现有理论中的波函数左右变换算符，不能经受住试金石的检验。
一经检验，真假立判。我们的判词是：
- 宇称算符被再一次证伪[8]，足见其肯定是冒牌货，不能表征左右变换下的波函数变换。在以后的文章中，我们还将作一个系统性说明：对左右变换下的所有物理量变换，宇称算符均不能加以表征。
2、经受住检验的、我们原创的波函数左右变换算符，就是左右变换下的波函数变换算符。
多少年来，物理学界一直没有人从名闻遐迩的式(6)出发，去具体推导一下粒子几率分布函数w(r,t)的变换；多少年来，人们一直将宇称变换这个冒牌货，认作左右变换下的波函数变换及物理量变换[9][10][11]——不能不说，这是一个颇为奇葩的理性迷误，令人费解，让人长叹。
2025年12月12日 初稿于北京家中
2025年12月16日 定稿于北京家中
参考文献与注释：
[1]镜像反映，是空间坐标反射变换的另一种形式；它与左右变换之间，仅差一个空间坐标的旋转变换。
[2]江棋生. 揭示宇称变换的真面目. 2025年11月23日发布于微信公众号“阿
斗凿墙”、《光传媒》和《民主中国》网刊.
[3]江棋生. 空间反演下的物理量变换与左右对称性[ OL]. 序号1513，自然科
学—物理学，中国预印本服务系统，国家科技图书文献中心网，2010.09.10.
在网上搜索一下，就能见到这篇文章；或去我的《科学网》博客，也能找到这篇文章.
[4]江棋生. 物理学分立对称性新论[M]. 武汉：汉斯出版社，2022:128-129,132,144.
汉斯出版社关于此书的荐读网页：
https://mp.weixin.qq.com/s/2rlTYJejUuWzWJLNZV7_aQ
- 西安交大高等数学教研室. 复变函数[M]. 北京：人民教育出版社，1978:3-4.
[6]复数的四种表示法是：点表示法，矢量表示法，三角表示法和指数表示法。
[7]对处在同一状态下的大量粒子而言，波函数模的平方与t时刻在空间r处单
位体积内找到粒子的数目成正比。也就是说，在波的强度为极大的地方，找到
粒子的数目为极大；在波的强度为零的地方，找到粒子的数目为零。
[8]在文献[2]中，我们运用左右变换下正确的速度变换公式，首次证伪了宇称变换。
[9]李政道. 粒子物理和场论[M]. 济南：山东科技出版社，1996：109.
[10]赖德 L. 基本粒子与对称性[M]. 北京：科学出版社，1980：26.
[11]JACKSON J D. 经典电动力学[M]. 北京：高等教育出版社，2003：271.
（文章仅代表作者的观点和立场）
